В прямоугольном треугольнике ABC ∠C = 90°, CH — высота, проведенная к гипотенузе, 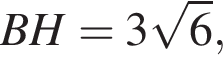 ∠BCH = 30°. Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
∠BCH = 30°. Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Длина стороны ВС треугольника АВС равна ...
Б) Длина стороны АС треугольника АВС равна ...
B) Расстояние от точки пересечения биссектрис треугольника ABC
до стороны AB равно ...
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) 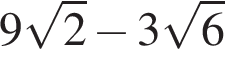
6) ![]()
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.

 и
и  Из прямоугольного треугольника CBA получаем
Из прямоугольного треугольника CBA получаем  и
и 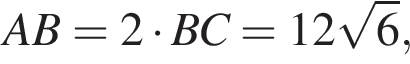 следовательно,
следовательно, 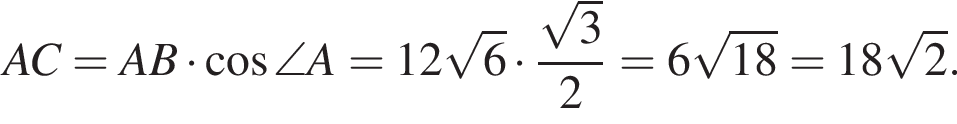
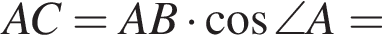
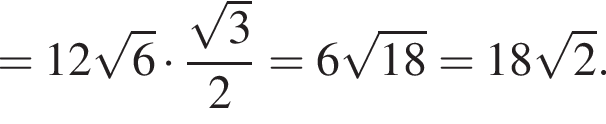
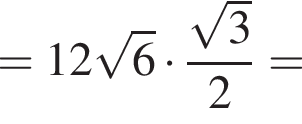
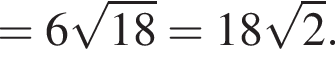
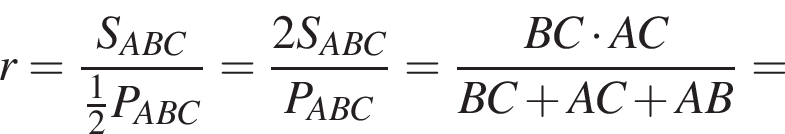
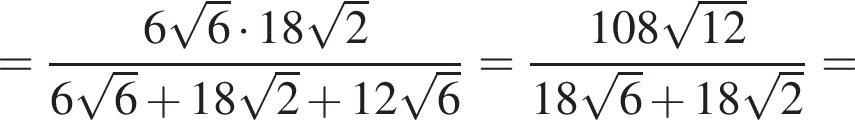
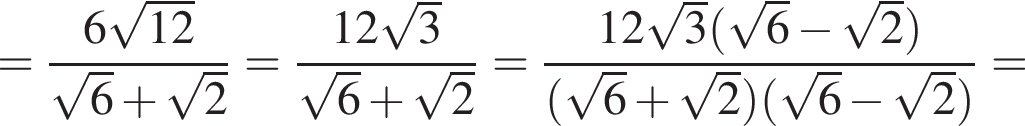
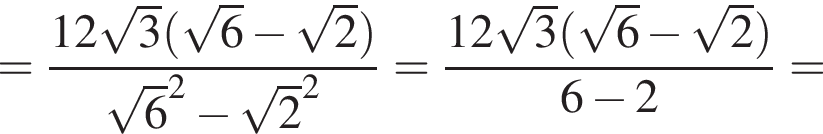
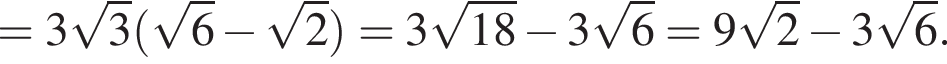
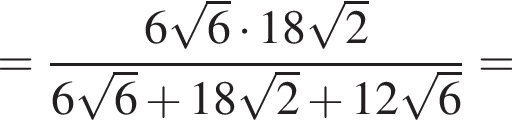
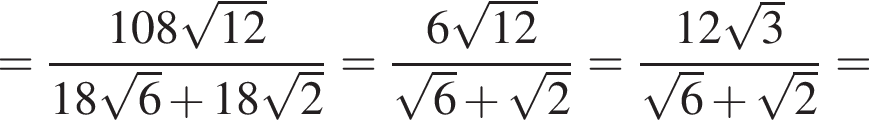
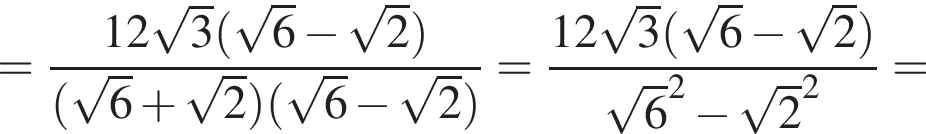
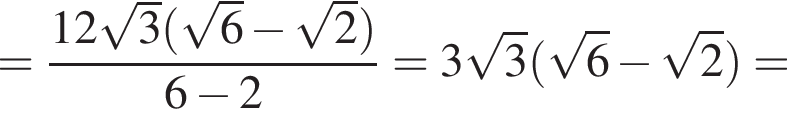
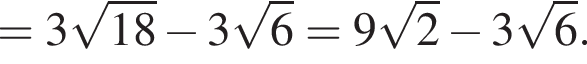
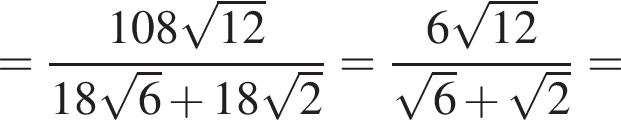
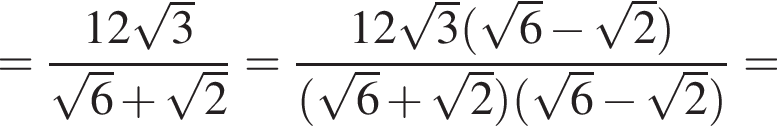

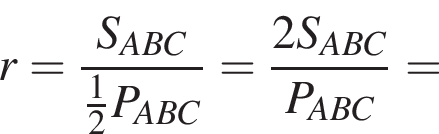
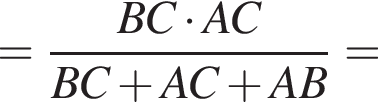
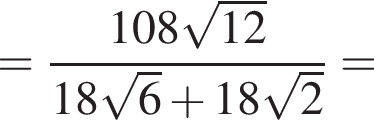
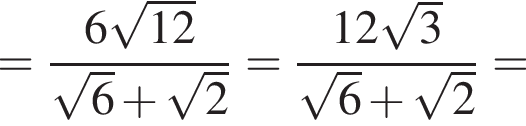
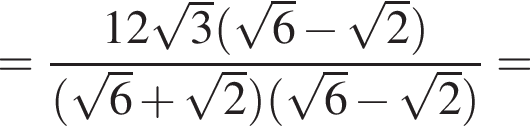
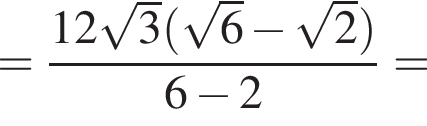
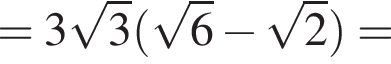
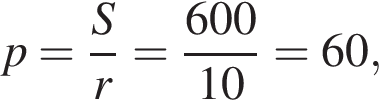 где p — полупериметр треугольника ABC, S — площадь треугольника, r — радиус вписанной окружности, откуда третья сторона треугольника равна
где p — полупериметр треугольника ABC, S — площадь треугольника, r — радиус вписанной окружности, откуда третья сторона треугольника равна  Из условия задачи имеем:
Из условия задачи имеем: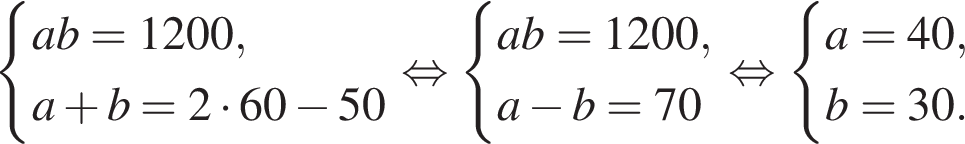
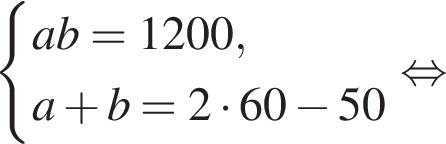
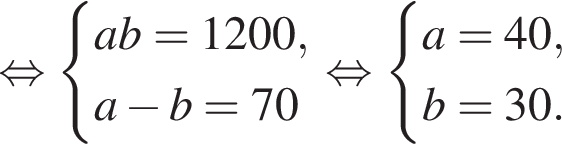
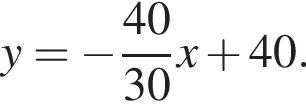 Уравнение окружности
Уравнение окружности 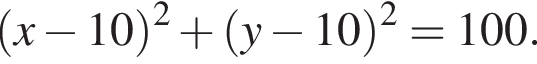 Получаем систему уравнений:
Получаем систему уравнений: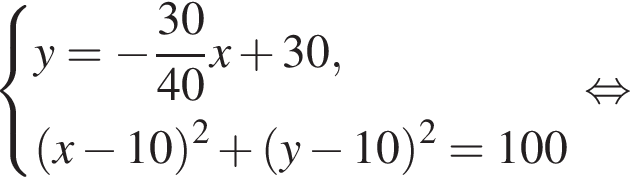
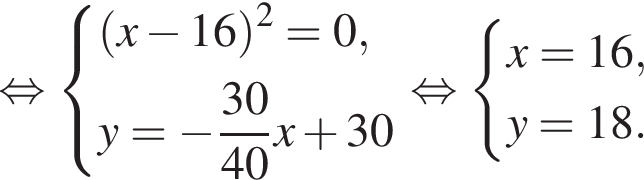
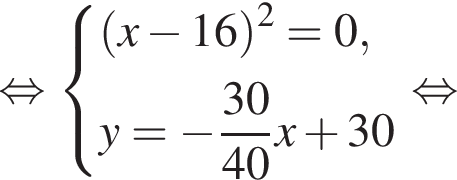
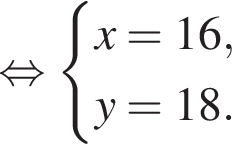
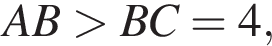 откуда
откуда  Разберем случаи.
Разберем случаи.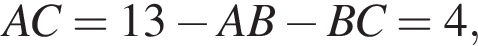 но тогда
но тогда 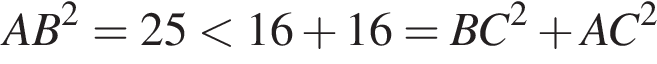
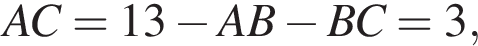 тогда
тогда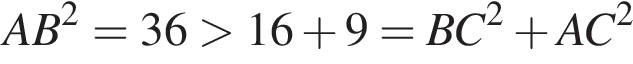
 то
то 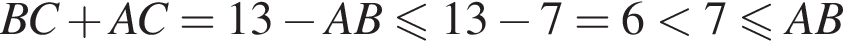
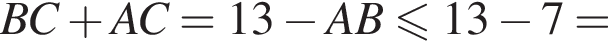
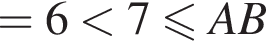
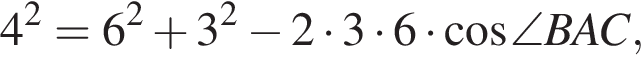
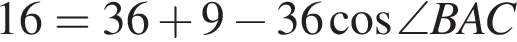 и
и 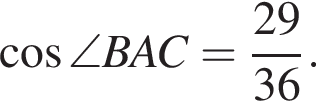
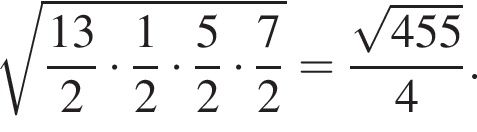
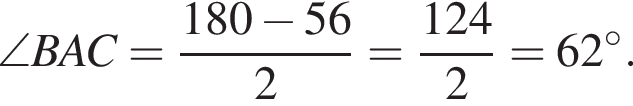
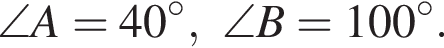 Укажите номер верного утверждения для сторон треугольника.
Укажите номер верного утверждения для сторон треугольника. Значит,
Значит,  — равнобедренный, а стороны AB и BC равны. Поскольку в треугольнике напротив большего угла лежит большая сторона, заключим, что
— равнобедренный, а стороны AB и BC равны. Поскольку в треугольнике напротив большего угла лежит большая сторона, заключим, что  и
и 
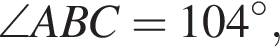
 Используя данные рисунка, найдите градусную меру угла ANM четырехугольника ABMN.
Используя данные рисунка, найдите градусную меру угла ANM четырехугольника ABMN. Так как сумма углов треугольника равна 180°,
Так как сумма углов треугольника равна 180°, 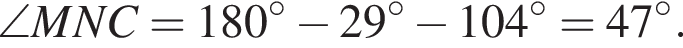 Угол ANM вертикальный с найденным. Значит, он равен
Угол ANM вертикальный с найденным. Значит, он равен 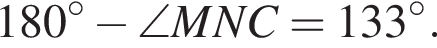

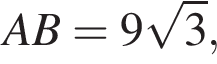
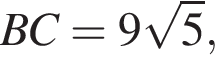 AD = DC.
AD = DC.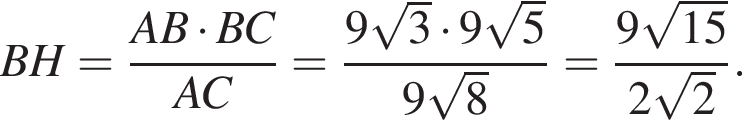
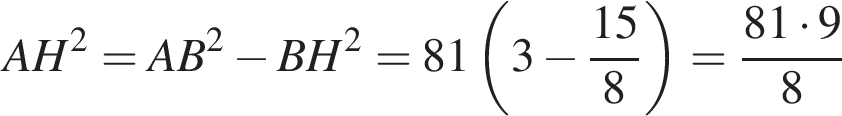
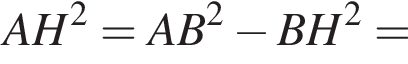
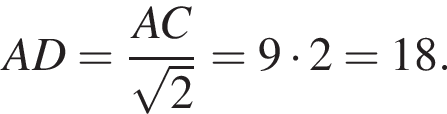
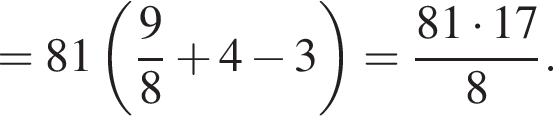


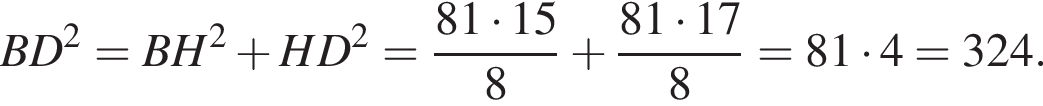

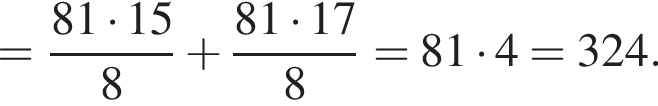
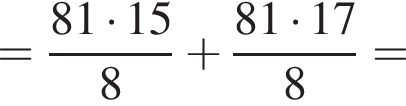
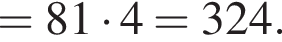
 CH и CK — высота и медиана соответственно, проведенные к гипотенузе (см. рис.). Найдите площадь прямоугольного треугольника ACB, если CK = 8,
CH и CK — высота и медиана соответственно, проведенные к гипотенузе (см. рис.). Найдите площадь прямоугольного треугольника ACB, если CK = 8, 
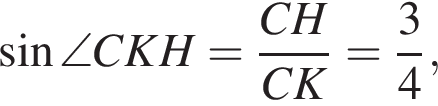 а CK = 8, получаем, что CH = 6. Отрезок CK — медиана прямоугольного треугольника, проведенная к гипотенузе, длина CK равна половине длины гипотенузы, тогда длина гипотенузы равна 2CK = 16. Площадь треугольника ACB равна
а CK = 8, получаем, что CH = 6. Отрезок CK — медиана прямоугольного треугольника, проведенная к гипотенузе, длина CK равна половине длины гипотенузы, тогда длина гипотенузы равна 2CK = 16. Площадь треугольника ACB равна 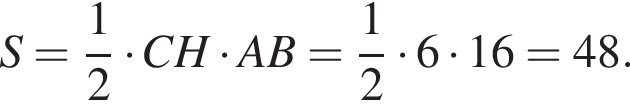
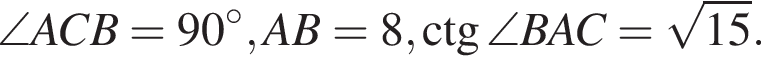 Найдите длину стороны CB.
Найдите длину стороны CB.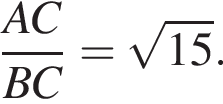 Из теоремы Пифагора:
Из теоремы Пифагора: Подставим одно выражение в другое и решим уравнение:
Подставим одно выражение в другое и решим уравнение: 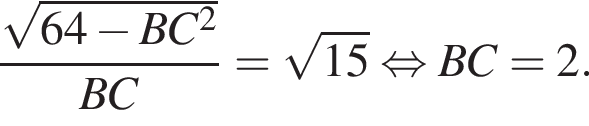
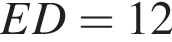 и радиус окружности, описанной вокруг AED равен 10.
и радиус окружности, описанной вокруг AED равен 10. Из соотношения
Из соотношения 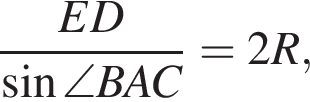
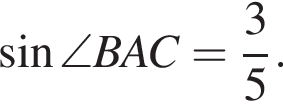
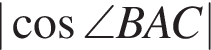 из основного тригонометрического тождества.
из основного тригонометрического тождества.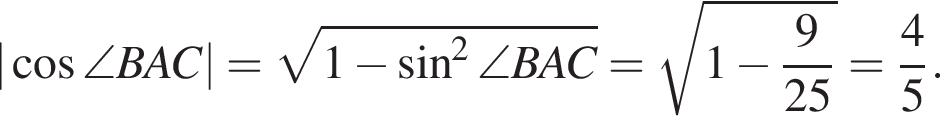
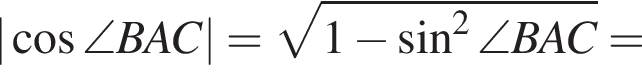
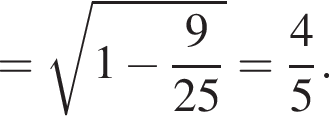
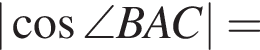
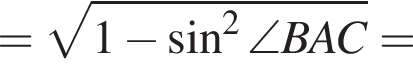
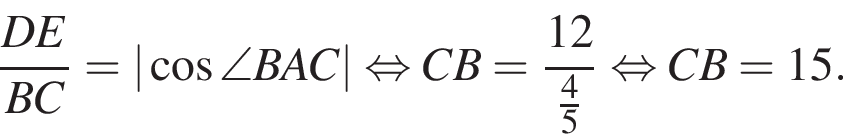
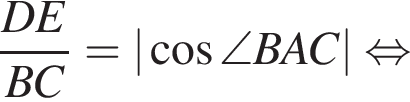
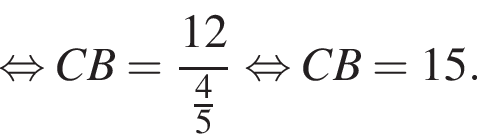
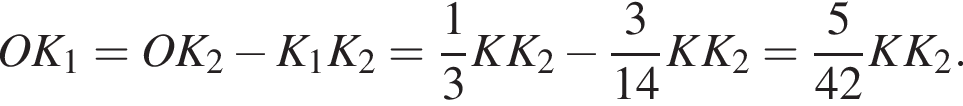
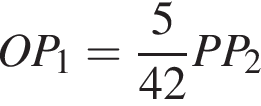 и
и 
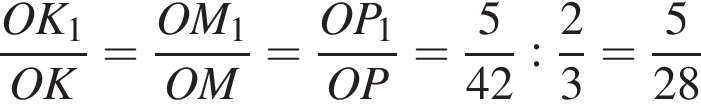 и треугольники M1K1P1 и MKP подобны, получаем
и треугольники M1K1P1 и MKP подобны, получаем 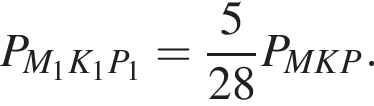 Тогда
Тогда 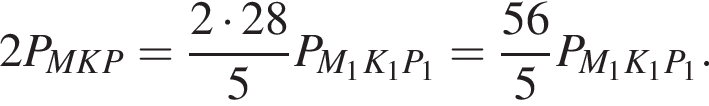 Тогда точка B обойдет периметр 56 раз.
Тогда точка B обойдет периметр 56 раз.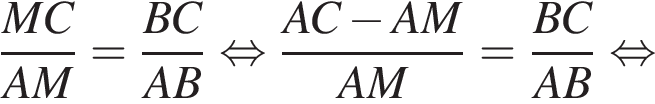
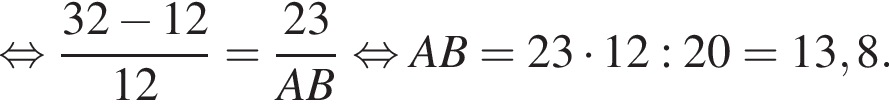
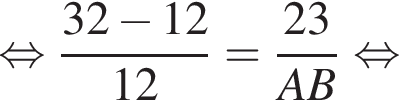
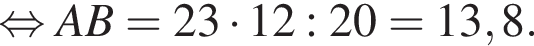
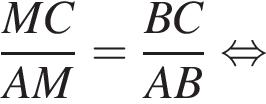
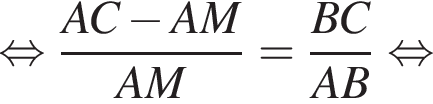
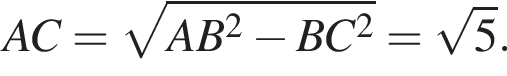 Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC
Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC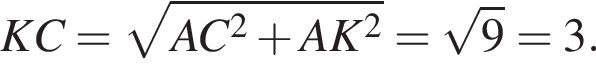

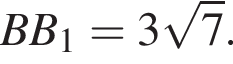
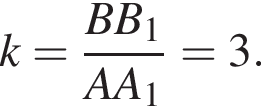 Известно, что
Известно, что 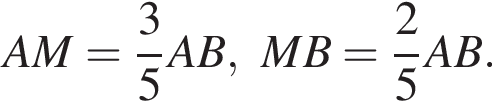 Тогда
Тогда 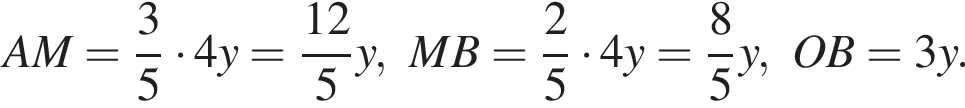
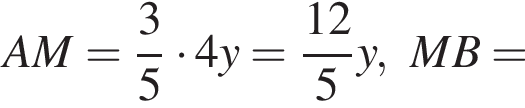
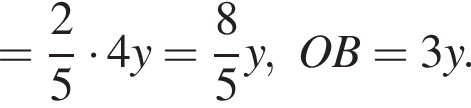
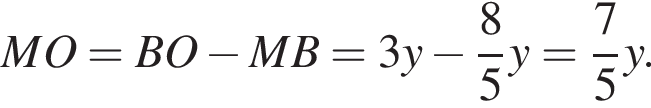 Из подобия треугольников имеем:
Из подобия треугольников имеем: 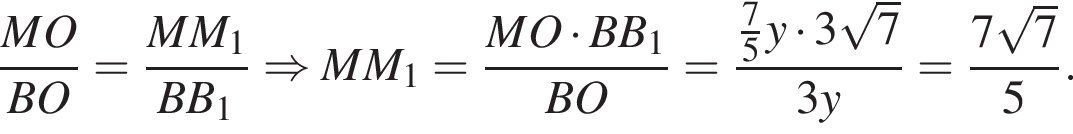
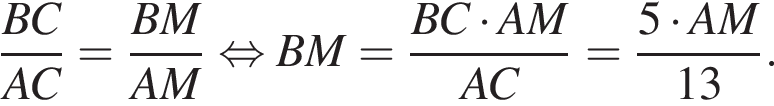
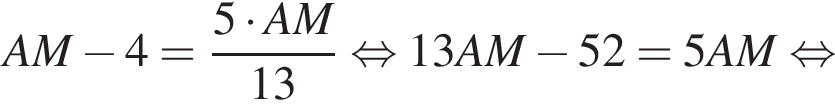
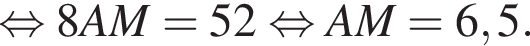
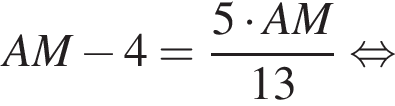

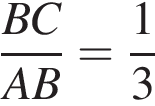 и
и 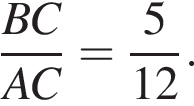 По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 14 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?
По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 14 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?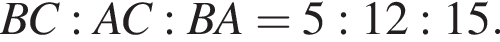 По свойству биссектрисы получаем, что
По свойству биссектрисы получаем, что 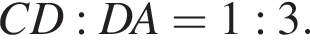 Значит, если
Значит, если  то
то 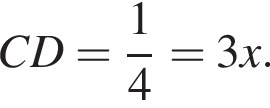
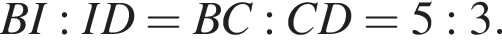 Значит, можно считать, что скорость первого тела равна 5υ, а второго 3υ. Время движения обратно пропорционально скорости, из условия следует, что
Значит, можно считать, что скорость первого тела равна 5υ, а второго 3υ. Время движения обратно пропорционально скорости, из условия следует, что 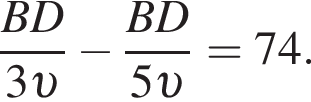
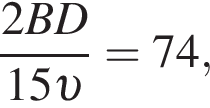 откуда
откуда 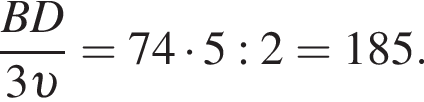
 BH и BK — высота и медиана соответственно, проведенные к гипотенузе (см. рис.). Найдите площадь прямоугольного треугольника ABC, если BK = 7,
BH и BK — высота и медиана соответственно, проведенные к гипотенузе (см. рис.). Найдите площадь прямоугольного треугольника ABC, если BK = 7, 
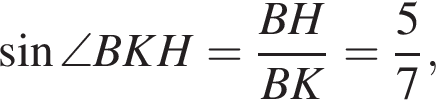 а BK = 7, получаем, что BH = 5. Отрезок BK — медиана прямоугольного треугольника, проведенная к гипотенузе, длина BK равна половине длины гипотенузы, тогда длина гипотенузы равна 2BK = 14. Площадь треугольника ABC равна
а BK = 7, получаем, что BH = 5. Отрезок BK — медиана прямоугольного треугольника, проведенная к гипотенузе, длина BK равна половине длины гипотенузы, тогда длина гипотенузы равна 2BK = 14. Площадь треугольника ABC равна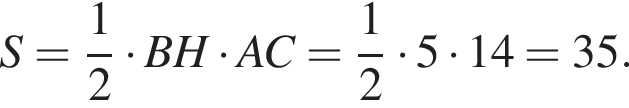
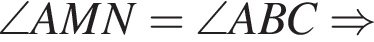
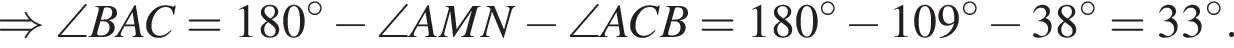
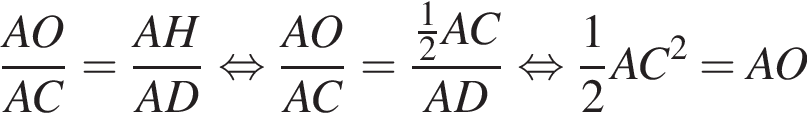
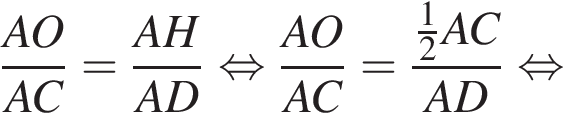
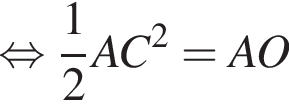

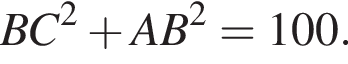 Площадь треугольника, с одной стороны, равна половине произведения катетов, а с другой — половина произведения высоты на сторону, к которой проведена высота. Имеем:
Площадь треугольника, с одной стороны, равна половине произведения катетов, а с другой — половина произведения высоты на сторону, к которой проведена высота. Имеем: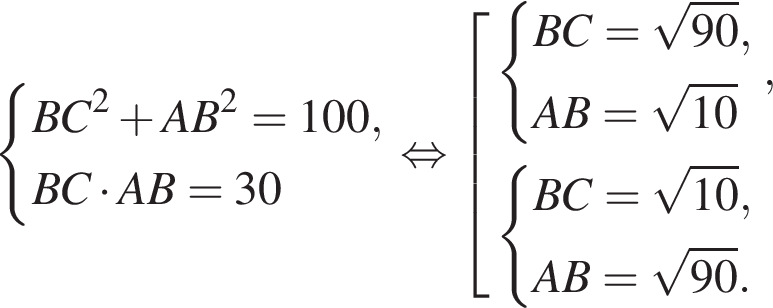
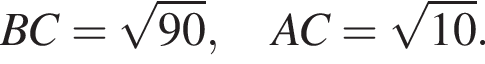 По теореме Пифагора найдем
По теореме Пифагора найдем 
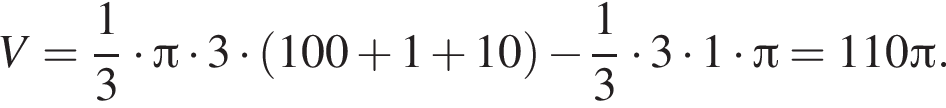
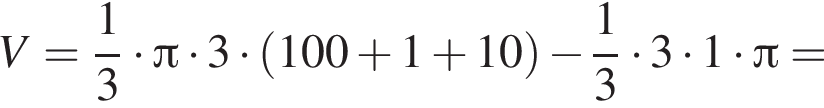
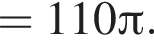
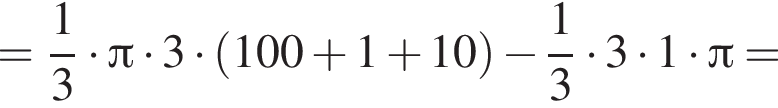




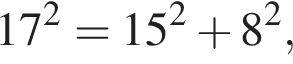 значит, треугольник прямоугольный.
значит, треугольник прямоугольный.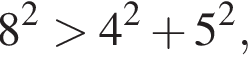 значит, треугольник тупоугольный.
значит, треугольник тупоугольный.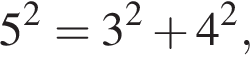 значит, треугольник прямоугольный.
значит, треугольник прямоугольный.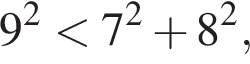 значит, треугольник остроугольный.
значит, треугольник остроугольный.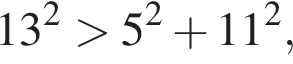 значит, треугольник тупоугольный.
значит, треугольник тупоугольный.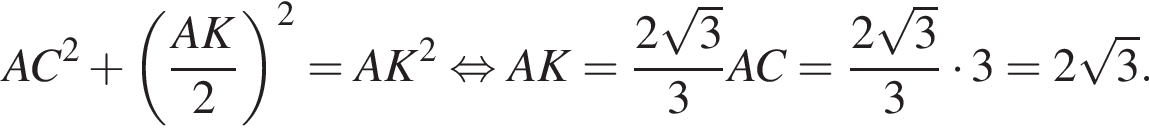
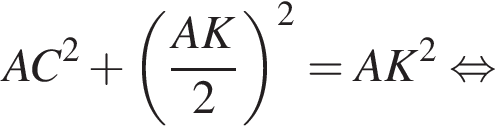
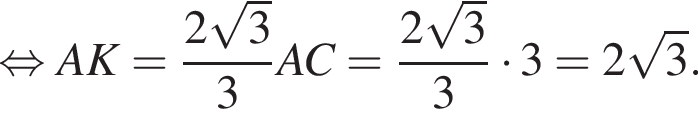
 — все углы разные.
— все углы разные. — все углы разные.
— все углы разные. — треугольник равнобедренный.
— треугольник равнобедренный. — все углы разные.
— все углы разные. — все углы разные.
— все углы разные.